class: center, middle, inverse, title-slide # L5: Modeling Part 1 ### Jean Morrison ### University of Michigan ### 2022-01-24 (updated: 2022-04-05) --- `\(\newcommand{\ci}{\perp\!\!\!\perp}\)` # Modeling - So far we have learned two strategies for estimating `\(E[Y(a)]\)` from data when we need to adjust for confounding or selection bias. - In IP weighting we re-weight our observations by `\(1/P[A = A_i \vert L_i]\)`, the probability that they received the treatment that they got given confounderts `\(L_i\)`. - In standardization, we first stratify the data by `\(L\)`, compute `\(E[Y \vert A = a, L]\)` within each stratum, and then take a weighted sum of these averages. - In both of these approaches, we have stayed totally non-parametric so far. --- # Non-Parametric Models - Our methods so far have been *non-parametric* because we haven't had to make any assumptions about the form of quantities like `\(E[Y \vert A, L]\)`. - We just estimate one value for every level of `\(A\)` and `\(L\)`. - This is also called a *saturated* model. - With this strategy, we can be sure that the true probability distribution is within th class we are searching. - So with enough data and the correct model, we will always converge to the true effect. --- # Limitations of Non-Parametric Models - Non-parametric models are limited in the complexity of data they can handle. - We can only handle variables with a small number of discrete levels. - We will need to make some assumptions to handle more complex data. - The validity of our inference will depend on these assumptions being correct. - But many parametric models are still flexible enough to do well. --- # NHEFS Data - Cigarette smokers aged 25-74 were recruited around 1971 and given a survey. - Ten years later, participants were given a followup survey. - We are interested in estimating the effect of quitting smoking on weight change on the additive scale. --- # Variables - Our exposure is binary (whether or not a person quit smoking between the first and second survey). - The outcome is the change in weight in kg. - What other features you would want to know in order to estimate the causal effect. -- - For now we will assume that the following variables are sufficient: + Sex (0: male, 1: female) + Age (in years) + Race (0: white, 1: other) + Education (5 categories) + Intensity of smoking (cigarettes per day) + Duration of smoking (years) + Physical activity in daily life (3 categories) + Recreational exercise (3 categories) + Weight (kg) --- # Limitations - We are only analyzing individuals who responded to the second survey. + For individuals who did not respond, we have neither exposure nor outcome data. + We will talk more about this later but for now are ignoring it. - Individuals may have quit at different times. + We could think of `\(A\)` as a time-varying treatment (coming up later). --- # Simple Analysis - The simplest analysis is to simply compare the mean weight change between quitters and non-quitters. <table> <thead> <tr> <th style="text-align:right;"> Quit Smoking </th> <th style="text-align:right;"> Average Weight Change </th> <th style="text-align:right;"> N </th> </tr> </thead> <tbody> <tr> <td style="text-align:right;"> 0 </td> <td style="text-align:right;"> 1.98 </td> <td style="text-align:right;"> 1163 </td> </tr> <tr> <td style="text-align:right;"> 1 </td> <td style="text-align:right;"> 4.53 </td> <td style="text-align:right;"> 403 </td> </tr> </tbody> </table> --- # Comparing Qitters and Non-Qitters <table> <thead> <tr> <th style="text-align:left;"> Variable </th> <th style="text-align:left;"> Did Not Quit Smoking </th> <th style="text-align:left;"> Quit Smoking </th> </tr> </thead> <tbody> <tr> <td style="text-align:left;"> Total </td> <td style="text-align:left;"> 1163 </td> <td style="text-align:left;"> 403 </td> </tr> <tr> <td style="text-align:left;"> Age, years </td> <td style="text-align:left;"> 42.8 (11.8) </td> <td style="text-align:left;"> 46.2 (12.2) </td> </tr> <tr> <td style="text-align:left;"> Female </td> <td style="text-align:left;"> 53.4% (621) </td> <td style="text-align:left;"> 45.4% (183) </td> </tr> <tr> <td style="text-align:left;"> Non-White </td> <td style="text-align:left;"> 14.6% (170) </td> <td style="text-align:left;"> 8.9% (36) </td> </tr> <tr> <td style="text-align:left;"> Cigarettes/day </td> <td style="text-align:left;"> 21.2 (11.5) </td> <td style="text-align:left;"> 18.6 (12.4) </td> </tr> <tr> <td style="text-align:left;"> Years smoking </td> <td style="text-align:left;"> 24.1 (11.7) </td> <td style="text-align:left;"> 26 (12.7) </td> </tr> <tr> <td style="text-align:left;"> Weight, kg </td> <td style="text-align:left;"> 70.3 (15.2) </td> <td style="text-align:left;"> 72.4 (15.6) </td> </tr> <tr> <td style="text-align:left;"> College </td> <td style="text-align:left;"> 9.9% (115) </td> <td style="text-align:left;"> 15.4% (62) </td> </tr> <tr> <td style="text-align:left;"> Little exercise </td> <td style="text-align:left;"> 37.9% (441) </td> <td style="text-align:left;"> 40.7% (164) </td> </tr> <tr> <td style="text-align:left;"> Inactive life </td> <td style="text-align:left;"> 8.9% (104) </td> <td style="text-align:left;"> 11.2% (45) </td> </tr> </tbody> </table> --- # Inverse Probability Weighting - Recall, the goal of IP weighting is to create a pseudo-population in which confounders `\(L\)` and treatment `\(A\)` are independent. - If `\(Y(a) \ci A \vert L\)`, then in the pseudo-population, `\(E[Y(a)] = E_{ps}[Y \vert A]\)`. - In the pseudo-population, association is causation, `$$E[Y(1)]-E[Y(0)] = E_{ps}[Y \vert A = 1] - E_{ps}[Y \vert A = 0]$$` --- # Estimating Weights - In our data, `\(L\)` is a vector of nine measurements. - We cannot compute `\(P[A = 1 \vert L ]\)` among every (or any) stratum of `\(L\)` because every participant has their own unique value of `\(L\)`. - We have to fit a parametric model. - What would you do? --- # Weights Estimated by Logistic Regression - We will use a logistic regression model to predict `\(P[A \vert L]\)` - The goal is to get the best possible estimate of the probability of treatment so we should fit a flexible model. ```r fit <- glm(qsmk ~ sex + race + age + I(age ^ 2) + as.factor(education) + smokeintensity + I(smokeintensity ^ 2) + smokeyrs + I(smokeyrs ^ 2) + as.factor(exercise) + as.factor(active) + wt71 + I(wt71 ^ 2), family = binomial(), data = dat) dat$w <- ifelse(dat$qsmk == 0, 1/(1 - predict(fit, type = "response")), 1/(predict(fit, type = "response"))) ``` ``` ## Min. 1st Qu. Median Mean 3rd Qu. Max. ## 1.054 1.230 1.373 1.996 1.990 16.700 ``` --- # Positivity - *Structural violations* of positivity occur when it is impossible for people with some levels of confounders to receive a particular level of treatment. + If we have structural violations, we cannot use IP weighting or standardization. + We need to restrict our inference to relevant strata of `\(L\)`. - *Random violations* of positivity occur when certain combinations of `\(L\)` and `\(A\)` are missing from our data by chance. + We are using a parametric model, so we are able to smooth over the zeroes. + We are able to predict for strata that were not observed in our data. + We should be careful about predicting outside the range of the observed data. --- # Horvitz-Thompson Estimator - The *Horvitz-Thompson estimator* is one of two options for estimating `\(E[Y(a)]\)` using our estimated weights. - The Horvitz-Thompson estimator just plugs our estimated weights into our previous formula. $$ \hat{E}[Y(a)] = \hat{E}\left[\frac{I(A = a)Y}{f(A\vert L)} \right] = \frac{1}{n}\sum_{i = 1}^n I(A_i = a)Y_i W_i $$ --- # Hajek Estimator - The *Hajek estimator* fits the linear model $$ E[Y \vert A] = \theta_0 + \theta_1 A $$ by weighted least squares, weighting individuals by our estimated IP weights. - It is is equivalent to `$$\frac{ \hat{E}\left[\frac{I(A = a)Y}{f(A\vert L)} \right]}{ \hat{E}\left[\frac{I(A = a)}{f(A\vert L)} \right]} = \frac{\sum_{i = 1}^n I(A_i = a)Y_i W_i}{\sum_{i = 1}^n I(A_i = a) W_i}$$` --- # Hajek Estimator - Hajek estimator is unbiased for `$$\frac{ E\left[\frac{I(A = a)Y}{f(A\vert L)} \right]}{ E\left[\frac{I(A = a)}{f(A\vert L)} \right]}$$` - Under positivity, $$ E\left[\frac{I(A = a)}{f(A\vert L)} \right] = 1 $$ - Guaranteed to be between 0 and 1 for dichotomous outcomes. - If positivity does not hold, the Hajek estimator is unbiased for `\(E[Y(a) \vert L \in Q(a)]\)`, where `\(Q(a)\)` is the set of values of `\(l\)` such that `\(P[A = a \vert L = l] > 0\)`. - Without positivity, the risk difference estimated by the Hajek estimator does not have a causal interpretation. --- # IP Weighted Effect Estimate in NHEFS ```r lm(wt82_71 ~ qsmk, data = dat, weights = w) ``` ``` ## ## Call: ## lm(formula = wt82_71 ~ qsmk, data = dat, weights = w) ## ## Coefficients: ## (Intercept) qsmk ## 1.780 3.441 ``` - We estimate that quitting smoking leads to a 3.4 kg increase in weight gain. --- # Estimating the Variance of the Estimate - The raw variance estimate from weighted least squares does not account for uncertainty in the weights. - We need to account for having estimated the IP weights. - Options: 1. Derive the variance analytically 2. Non-parametric bootstrapping (more details later) 3. Robust sandwich variance estimate. - Option 3 is conservative but easier than options 1 and 2. - Option 3 can be achieved by fitting with GEE using and independent working correlation matrix or using the `HC0` option in `vcovHC`. --- # Variance Estiamte in the NHEFS Data ```r library("geepack") msm.w <- geeglm(wt82_71 ~ qsmk, data = dat,weights = w, id = seqn,corstr = "independence") beta <- coef(msm.w) SE <- coef(summary(msm.w))[, 2] lcl <- beta - qnorm(0.975) * SE ucl <- beta + qnorm(0.975) * SE cbind(beta, lcl, ucl) ``` ``` ## beta lcl ucl ## (Intercept) 1.779978 1.339514 2.220442 ## qsmk 3.440535 2.410587 4.470484 ``` --- # Stabilized Weights - Using weights `\(W^{A} = 1/f(A \vert L)\)` we create a pseudo-population in which (heuristically), each person is matched by someone exactly like them who received the opposite treatment. - Our pseudo-population is twice as big as our actual sample so the mean of `\(W^A\)` is 2. - In the pseudo-population, the frequency of treatment `\(A = 1\)` is 50%. - We could have created other pseudo-populations. --- # Stabilized Weights - Our requirements are that, in the pseudo-population, probability of treatment is independent of `\(L\)`. - But different people could have different probabilities of treatment. - To create stabilized weights, we construct a pseudo-population in which the probability of receiving each treatment is the same as the frequency of the treatment in our original sample. $$ SW^A = \frac{f(A)}{f(A \vert L)} $$ --- # Stabilized Weights - In our data, `\(A\)` is binary, so we can compute `\(f(1)\)` as the proportion of quitters in the data. ```r p1 <- mean(dat$qsmk); p1 ``` ``` ## [1] 0.2573436 ``` - In the pseudo-population created by the stabilized weights, person in our data set corresponds to 26% of a treated person and 74% of an untreated person. ```r dat <- dat %>% mutate(pa = ifelse(dat$qsmk == 0, 1-p1, p1), sw= pa*w) summary(dat$sw) ``` ``` ## Min. 1st Qu. Median Mean 3rd Qu. Max. ## 0.3312 0.8665 0.9503 0.9988 1.0793 4.2977 ``` - The expected value of `\(SW^A\)` is 1 because the pseudo-population is the same size as the observed data. --- # Estimation Using the Stabilized Weights ```r msm.sw <- geeglm(wt82_71 ~ qsmk,data = dat, weights = sw, id = seqn,corstr = "independence") beta <- coef(msm.w) SE <- coef(summary(msm.sw))[, 2] lcl <- beta - qnorm(0.975) * SE ucl <- beta + qnorm(0.975) * SE cbind(beta, lcl, ucl) ``` ``` ## beta lcl ucl ## (Intercept) 1.779978 1.339514 2.220442 ## qsmk 3.440535 2.410587 4.470484 ``` - These are exactly the results we saw with the unstabilized weights. --- # Why Use Stabilized Weights - Differences between stabilized and non-stabilized weights only occur when the model for `\(E[Y \vert A]\)` is not saturated. - When the model is not saturated, stabilized weights typically result in greater efficiency. --- # Marginal Structural Models - In the IP weighting strategy we create a population in which `\(A\)` is indepedent of `\(L\)` and then fit the model `$$E_{ps}[Y \vert A ] = \theta_0 + \theta_1 A$$` - If we believe our conditional exchangeability assumption `\(Y(a) \ci A \vert L\)`, then in the pseudo-population, `\(E_{ps}[Y \vert A] = E[Y(a)]\)`. - So the parameter `\(\theta_1\)` is interpretable as the causal risk difference. -- - We have proposed a model for the average counterfactual: `$$E[Y(a)] = \beta_0 + \beta_1 a$$` -- - This model is *marginal* because we have marginalized (averaged) over the values of all other covariates. - It is structural because it is a model for a counterfactual `\(E[Y(a)]\)` rather than a probability distribution `\(E[Y \vert A]\)`. --- # Modeling Continuous Treatments - Because out treatment was binary, we could construct a saturated model. - For continuous (or highly polytomous) variables, we can't do that and will have to use a parametric model instead. - In the NHEFS data, let `\(A\)` be the change in smoking intensity ( `\(A = 10\)` indicates that a person increased their smoking by 10 cigarettes). - We will limit to only those who smoked 25 or fewer cigarettes per day at baseline ( `\(N = 1,162\)` ) - We can propose a model for our *dose-response curve* $$ E[Y(a)] = \beta_0 + \beta_1 a + \beta_2 a^2 $$ --- # Estimating Weights for the Continuous Treatment - To use stabilized weights, we need to estimate `\(f(A \vert L)\)` and `\(f(A)\)`. - Both of these are PDFs which are hard to estimate! - We will assume that both `\(f(A \vert L)\)` and `\(f(A)\)` are normal with constant variance across participants. - We will estimate the mean of `\(f(A \vert L)\)` via linear regression. - These assumptions are almost certainly wrong. - IP weighted estimates of continuous variables can be very sensitive to choice of weights. --- # Estimating Weights for the Continuous Treatment - We fit a linear model for change in smoking intensity including: + sex, race, education, exercise, life activity + age and age squared + baseline smoking intensity and baseline smoking intensity squared + baseline weight and baseline weight squared - The fitted values of this model give the mean of `\(f(A \vert L)\)`. - We can use the variance of the residuals as an estimate of the variance of `\(f(A \vert L)\)` - We then compute `\(f(A \vert L)\)` using `dnorm`. --- # Estimating Weights for the Continuous Treatment - To estimate `\(f(A)\)` we use the same procedure, except that the mean of `\(f(A)\)` is is just the sample proportion of treated or untreated participants. - For comparison, we compute both the standardized weights and the non-standardized weights ```r summary(dat.s$sw_cont) ``` ``` ## Min. 1st Qu. Median Mean 3rd Qu. Max. ## 0.1938 0.8872 0.9710 0.9968 1.0545 5.1023 ``` ```r summary(dat.s$w_cont) ``` ``` ## Min. 1st Qu. Median Mean 3rd Qu. Max. ## 25.4 26.4 30.0 1078.1 47.5 428611.4 ``` - The non-standardized weights are much more variable! --- # Fitting the Continuous Treatment Model - We then fit the marginal structural model $$ E[Y(a)] = \beta_0 + \beta_1 a + \beta_2 a^2$$ using exactly the same strategy we used before. <table> <thead> <tr> <th style="empty-cells: hide;border-bottom:hidden;" colspan="1"></th> <th style="border-bottom:hidden;padding-bottom:0; padding-left:3px;padding-right:3px;text-align: center; " colspan="2"><div style="border-bottom: 1px solid #ddd; padding-bottom: 5px; ">Stabilized Weights</div></th> <th style="empty-cells: hide;border-bottom:hidden;" colspan="1"></th> <th style="border-bottom:hidden;padding-bottom:0; padding-left:3px;padding-right:3px;text-align: center; " colspan="2"><div style="border-bottom: 1px solid #ddd; padding-bottom: 5px; ">Non-Stabilized Weights</div></th> </tr> <tr> <th style="text-align:left;"> </th> <th style="text-align:left;"> Estimate </th> <th style="text-align:left;"> 95% CI </th> <th style="text-align:left;"> </th> <th style="text-align:left;"> Estimate </th> <th style="text-align:left;"> 95% CI </th> </tr> </thead> <tbody> <tr> <td style="text-align:left;"> Intercept </td> <td style="text-align:left;"> 2 </td> <td style="text-align:left;"> (1.4, 2.6) </td> <td style="text-align:left;"> </td> <td style="text-align:left;"> 7.7 </td> <td style="text-align:left;"> (1, 14) </td> </tr> <tr> <td style="text-align:left;"> Smk Int </td> <td style="text-align:left;"> -0.11 </td> <td style="text-align:left;"> (-0.17, -0.047) </td> <td style="text-align:left;"> </td> <td style="text-align:left;"> 0.1 </td> <td style="text-align:left;"> (-0.21, 0.42) </td> </tr> <tr> <td style="text-align:left;"> Smk Int Squared </td> <td style="text-align:left;"> 0.0027 </td> <td style="text-align:left;"> (-0.002, 0.0074) </td> <td style="text-align:left;"> </td> <td style="text-align:left;"> -0.01 </td> <td style="text-align:left;"> (-0.024, 0.0039) </td> </tr> </tbody> </table> --- # Continuous Model Results 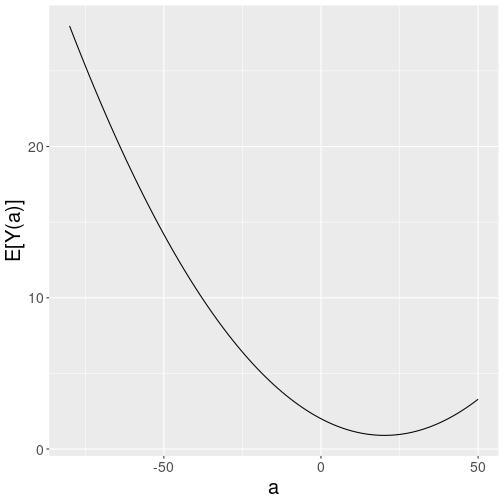<!-- --> --- # Issues with the Continuous Treatment Model - We had to make strong assumptions about the distribution of `\(A \vert L\)`. - There are structural positivity issues -- it is not possible for everyone to reduce their smoking by 80 cigarettes per day. --- # Effect Modification in Marginal Structural Models - We might be interested in estimating the causal effect within strata of `\(V\)`. - We can propose a marginal structural model that includes `\(V\)` $$ E[Y(a) \vert V] = \beta_0 + \beta_1 a + \beta_2 a V + \beta_3 V $$ - If `\(V\)` and `\(A\)` are both dichotomous, this model is saturated. - It is not really fully marginal any more, but we still call it a marginal structural model. --- # Interpreting Parameters in the Effect Modification Model - Suppose that `\(V\)` is sex (0: Male, 1: Female) and `\(A\)` is quitting/not quitting. $$ E[Y(a) \vert V] = \beta_0 + \beta_1 a + \beta_2 a V + \beta_3 V $$ - `\(\beta_1\)` is the causal effect of quitting for men. - `\(\beta_1+ \beta_2\)` is the causal effect of quitting for women. - What is `\(\beta_3\)`? -- - `\(\beta_3\)` is not a causal parameter because we haven't made any exchangeability assumptions about `\(V\)`. - `\(\beta_3\)` is the difference between `\(E[Y(0)]\)` in females and `\(E[Y(0)]\)` in males but is not the causal effect of sex. --- # Stablilized Weights for the EM Model - We have two choices for stabilized weights $$ \frac{f(A)}{f(A \vert L)} \qquad \text{or} \qquad \frac{f(A\vert V)}{f(A \vert L)} $$ - Which will be more efficient? -- - Conditioning on `\(V\)` in the numerator will make the numerator closer to the denominator. - The second choice of weights will be less variable. - So the second choice of weights is more efficient. --- # Stablilized Weights for the EM Model - We need to compute `\(f(A \vert V)\)` in our data. - We can just use the stratified means. ```r fav_fit <- lm(qsmk ~ sex, data = dat) dat$pav <- ifelse(dat$qsmk == 0, 1-predict(fav_fit, type = "response"), predict(fav_fit, type = "response")) dat <- mutate(dat, sw_em = pav*w) summary(dat$sw_em) ``` ``` ## Min. 1st Qu. Median Mean 3rd Qu. Max. ## 0.2930 0.8751 0.9554 0.9989 1.0803 3.8011 ``` --- # Fitting the Effect Modification Model ```r msm.emm <- geeglm( wt82_71 ~ qsmk*sex, data = dat, weights = sw_em, id = seqn, corstr = "independence") beta <- coef(msm.emm) SE <- coef(summary(msm.emm))[, 2] lcl <- beta - qnorm(0.975) * SE ucl <- beta + qnorm(0.975) * SE cbind(beta, lcl, ucl) ``` ``` ## beta lcl ucl ## (Intercept) 1.784446876 1.1771686 2.3917252 ## qsmk 3.521977634 2.2341453 4.8098100 ## sex -0.008724784 -0.8883884 0.8709389 ## qsmk:sex -0.159478525 -2.2097583 1.8908013 ``` - We have no strong evidence of effect modificaiton by sex. --- # Unweighted Regression vs IP Weighting - What if we had conditioned on every variable in `\(L\)`? - The stabilized weights would be 1, so we would just be running a regular regression. - If we believe in the model for `\(E[Y(a) \vert L]\)`, then the regression coefficient is interpretable as a (conditional) causal parameter. - Using the marginal model with IP weighting, we need to believe that our estimates of `\(f(A \vert L)\)` are accurate. - In some cases, solving a prediction problem is easier than guessing the correct structural model for all confounders. --- # Censoring and Missing Data With IP Weights - In our analysis, we have removed 63 individuals who filled in the survey in 1982 but who have a missing value for weight. <table> <thead> <tr> <th style="text-align:right;"> Quit Smoking </th> <th style="text-align:right;"> Number Missing </th> <th style="text-align:right;"> Percent Missing </th> </tr> </thead> <tbody> <tr> <td style="text-align:right;"> 0 </td> <td style="text-align:right;"> 38 </td> <td style="text-align:right;"> 3.2 </td> </tr> <tr> <td style="text-align:right;"> 1 </td> <td style="text-align:right;"> 25 </td> <td style="text-align:right;"> 5.8 </td> </tr> </tbody> </table> - We have more missing data for people who quit smoking than people who did not, so we could have selection bias. --- # Weights for Censoring - We learned in L4 that, to correct for selection bias, we need to find a set of variables `\(L_c\)` such that `\(Y(C = 0) \ci C \vert L_c\)`. - We then need to estimate `\(W^C = 1/P[C = 0 \vert A, L_c]\)`, or the stabilized version `$$SW^C = \frac{P[C = 0 \vert A]}{P[C = 0 \vert A, L_c]}$$` - We will use the same set of variables, we used to compute weights for confounding. - The total weights will be `\(SW^C \cdot SW^A\)` --- # Weights for Censoring - We will estimate `\(f(C=0 \vert A, L)\)` using a logistic model adjusting for + the exposure + sex, race age, education, exercise, life activity + linear and quadratic terms for smoking intensity, duration, and baseline weight. - We can estimate `\(f(C = 0 \vert A)\)` using the average within levels of `\(A\)`. + Summarizing `\(SW^C\)` ```r summary(dat$sw.c) ``` ``` ## Min. 1st Qu. Median Mean 3rd Qu. Max. ## 0.9442 0.9782 0.9858 0.9990 1.0035 1.7180 ``` - And the combined weights ```r summary(dat$sw.comb) ``` ``` ## Min. 1st Qu. Median Mean 3rd Qu. Max. ## 0.3390 0.8593 0.9442 0.9974 1.0749 4.1829 ``` --- # Combined Weights Results - Below are results using the combined weights for both censoring and confounding <table> <thead> <tr> <th style="text-align:left;"> </th> <th style="text-align:left;"> Estimate </th> <th style="text-align:left;"> 95% CI </th> </tr> </thead> <tbody> <tr> <td style="text-align:left;"> Intercept </td> <td style="text-align:left;"> 1.69 </td> <td style="text-align:left;"> (1.23, 2.14) </td> </tr> <tr> <td style="text-align:left;"> Quit Smoking </td> <td style="text-align:left;"> 3.4 </td> <td style="text-align:left;"> (2.36, 4.45) </td> </tr> </tbody> </table> - Compared with the previous results <table> <thead> <tr> <th style="text-align:left;"> </th> <th style="text-align:left;"> Estimate </th> <th style="text-align:left;"> 95% CI </th> </tr> </thead> <tbody> <tr> <td style="text-align:left;"> Intercept </td> <td style="text-align:left;"> 1.78 </td> <td style="text-align:left;"> (1.34, 2.22) </td> </tr> <tr> <td style="text-align:left;"> Quit Smoking </td> <td style="text-align:left;"> 3.44 </td> <td style="text-align:left;"> (2.41, 4.47) </td> </tr> </tbody> </table> --- # Standardization - Recall from previous lectures (and homework) that IP weighting and standardization were equivalent when we could be fully non-parametric. - Our standardization formula is $$ E[Y(a)] = \sum_l P[Y \vert A = a, L = l]P[L = l] $$ - In our example, `\(L\)` is continuous, so we need to integrate $$ E[Y(a)] = \int_l P[Y \vert A = a, L = l]f(l) dl $$ --- # Outcome Modeling - In the standardization formula, we need to estimate `\(P[Y \vert A = a, L = l]\)`. - To do this we fit a linear regression ```r fit <-glm( wt82_71 ~ qsmk + sex + race + age + I(age * age) + as.factor(education) + smokeintensity + I(smokeintensity * smokeintensity) + smokeyrs + I(smokeyrs * smokeyrs) + as.factor(exercise) + as.factor(active) + wt71 + I(wt71 * wt71) + qsmk * smokeintensity, data = dat.u) summary(fit)$coefficients %>% head() ``` ``` ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) -1.588165662 4.313035924 -0.3682245 0.7127562582 ## qsmk 2.559594093 0.809148613 3.1633177 0.0015901758 ## sex -1.430271659 0.468957553 -3.0498958 0.0023281370 ## race 0.560109604 0.581888778 0.9625716 0.3359131882 ## age 0.359635262 0.163318764 2.2020450 0.0278094360 ## I(age * age) -0.006100955 0.001726136 -3.5344591 0.0004206537 ``` --- # Outcome Modeling - This first step of fitting the outcome model is just fitting a regular linear regression. - If we believe the outcome model is correct and includes all confounders, we can use the outcome regression to estimate the ATE. - However, the regression we fit included an interaction between `\(A\)` and a covariate, smoking intensity. + With no interaction, the coefficient on `\(A\)` would estimate the ATE (if the model were correct). + A model with no interaction says that the treatment effect is constant across levels of `\(L\)`. - With the interaction, the coefficient on `\(A\)` is only the ATE within strata defined by smoking intensity (the conditional effect). - To estimate the (marginal) average treatment effect, we need to average over levels of `\(L\)`. --- # Standardizing - Fortunately, we do not need to compute `\(f(l)\)`. - Using the double expectation, we can write $$ \int_l P[Y \vert A = a, L = l]f(l)dl = E\left[ E\left[Y \vert A = a, L = l \right]\right] $$ - So we can estimate the standardized mean as $$ \frac{1}{n}\sum_{i=1}^n\hat{E}[Y \vert A = a, L_i] $$ --- # Standardizing - For each person, we need to compute two values `\(\hat{E}[Y \vert A = 0, L_i]\)` and `\(\hat{E}[Y\vert A = 1, L_i]\)` - These are predicted values that we can get out of our previous regression. - We predict each person's outcome with `\(A = 0\)` and with `\(A = 1\)`. ```r dat0 <- dat1 <- dat.u dat0$qsmk <- 0 dat1$qsmk <- 1 Y0 <- predict(fit, newdata = dat0, type = "response") %>% mean() Y1 <- predict(fit, newdata = dat1, type = "response") %>% mean() cat(round(Y1, digits = 2), "-", round(Y0, digits = 2), "=", round(Y1-Y0, digits = 2)) ``` ``` ## 5.18 - 1.66 = 3.52 ``` --- # Censoring - In our case, we have assumed that our set of confounders are also sufficient to adjust for censoring. - In the previous step, we predicted weight gain for all subjects, even those who had missing values in the original data. - If our outcome model is correct *and* `\(Y(C = 0) \ci C \vert L\)`, then this is sufficient to eliminate selection bias. --- # Estimating the Variance - To compute the variance of the estimate, we need to bootstrap. - We will repeatedly re-sample our data with replacement. - Each time, we recompute the standardized effect we just computed in the observed data. - The standard deviation of our bootstrap samples consistently estimates the standard error of our estimate. --- # Bootstrapping the Variance ```r set.seed(1) samples <- replicate(n = 500, expr = sample(seq(nrow(dat.u)), size = nrow(dat.u), replace = TRUE)) res <- apply(samples, 2, FUN = function(ix){ boot_dat <- dat.u[ix,] boot_fit <-glm( wt82_71 ~ qsmk + sex + race + age + I(age * age) + as.factor(education) + smokeintensity + I(smokeintensity * smokeintensity) + smokeyrs + I(smokeyrs * smokeyrs) + as.factor(exercise) + as.factor(active) + wt71 + I(wt71 * wt71) + qsmk * smokeintensity, data = boot_dat) boot_dat0 <- boot_dat1 <- boot_dat boot_dat0$qsmk <- 0 boot_dat1$qsmk <- 1 bootY0 <- predict(boot_fit, newdata = boot_dat0, type = "response") %>% mean() bootY1 <- predict(boot_fit, newdata = boot_dat1, type = "response") %>% mean() return(bootY1 - bootY0) }) se <- sd(res) ci <- (Y1-Y0) + c(-1, 1)*qnorm(0.975)*se cat(Y1-Y0, "(", ci, ")") ``` ``` ## 3.518574 ( 2.576592 4.460556 ) ``` --- # Effect Modification in Standardization - If we want to estimate the average causal effect stratified by `\(V\)`, we can simply stratify by `\(V\)` before averaging our predicted values. ```r dat.u$Y0 <- predict(fit, newdata = dat0, type = "response") dat.u$Y1 <- predict(fit, newdata = dat1, type = "response") dat.u %>% group_by(sex) %>% summarize(Y0 = mean(Y0), Y1 = mean(Y1)) ``` ``` ## # A tibble: 2 × 3 ## sex Y0 Y1 ## <dbl> <dbl> <dbl> ## 1 0 1.66 5.30 ## 2 1 1.66 5.06 ``` --- # g-formula - The formula we have seen for standardization is called the `\(g\)`-formula (g is for generalized) $$ E[Y(a)] = \sum_l P[Y \vert A = a, L = l]P[L = l] $$ - The standardization and IP weighting estimation strategies are both making use of the g-formula. + Standardization is a "plug-in" estimator because we just plug estimates of `\(P[Y \vert A, L]\)` into the formula. --- # IP Weighting vs Standardization - When we are non-parametric, IP weighting and standardization are the same. - In parametric models, they rely on different assumptions and so are not the same. - In the IP weighted analysis, we need to trust our model for `\(f(A \vert L)\)`. - In the standardized analysis, we need to trust our model for `\(E[Y \vert A, L]\)`. - In either case, if our our parametric models are wrong, our predictions will be biased and so our estimators will be biased. - The amount of bias depends on how bad our predictions are. - We can compute both estimates and compare. --- # Doubly Robust Estimators - In doubly robust models, we need a model for both exposure and outcome, but we only need to get one model right. - One simple variation: + Estimate IP weights `\(W^A\)` using the exposure model. + Create a new covariate, `\(R\)`, equal to `\(W^A\)` if `\(A = 1\)` and `\(-W^A\)` if `\(A = 0\)`. + Fit an outcome model including the exposure, the confounders, *and* R. + Use the predicted values to estimate the standardized mean. - The standardized mean is now consistent for the causal effect if either model was correct. - Even when both estimates are wrong, the bias of the doubly robust estimator is smaller than the bias of the either the IP weighted or standardized estimator. - More on DR estimators coming up.